"Терпеть не могу математику", - обычно с таким настроем приходят на урок мои ученики. Последние два с половиной года я преподаю математику для трудных подростков от 14 до 20 лет. Как правило, они попадают в наше заведение, если совсем не справляются с нагрузкой в обычных школах. От них уже мало чего ждут, поэтому у учителей есть возможность пробовать новые форматы, чтобы хоть как-то увлечь подростков учебой.

Как-то я задумался, а как бы эти ребята отнеслись к предмету, если бы увидели математику с другой стороны – проблемы, которые будут им понятны и близки, работу в команде над общим решением, а в конце занятия они получали нужный им результат и гордились собой? Я решил, что мой любимый кубик Рубика мог бы мне помочь сделать обучение проще, а также укрепить связи внутри класса. С его помощью я планировал развить у ребят критическое мышление и научить их работе с алгоритмами.

Связываем кубик и математику воедино

Работа на уроках с кубиком Рубика позволила вести с классом неформальные математические беседы. Когда ученику удавалось собрать одну из граней кубика, с ним уже можно было начинать говорить о понятии трехмерности и объемных фигурах.

В определенные моменты я задавал и другие, связанные с математикой, вопросы: «На сколько процентов закончена сборка кубика?» или «Если каждый из трех учеников способен за две минуты собрать по грани кубика, за какой промежуток времени они вместе смогут собрать кубик целиком?»

Я хотел, чтобы ученики использовали и развивали навыки подсчета и установления причинно-следственных связей, и при этом им было весело. Я не стал заставлять производить все расчеты на бумаге, я хотел, чтобы они развивали навыки ментальной арифметики и сравнения – эти навыки будут полезны при дальнейшем изучении математики.

Кубик Рубика можно использовать, чтобы сформировать и закрепить знания учеников о двумерных и трехмерных объектах. Также кубик пригодится при изучении долей и фракций, отношений и пропорций. Например, на одной грани разобранного кубика Рубика могут одновременно находиться три красных, один синий, два зеленых, два желтых и один оранжевый квадраты. Учитель может спросить: «Какую часть грани занимают красные квадраты?»

Ученикам постарше учитель может на примере кубика показать понятие факториала, чтобы объяснить 43,252,003,274,489,856,000 различных комбинаций в кубике. Не имеет значения, насколько запутан кубик, найти решения всегда можно за 20 или менее шагов – этот факт всегда возбуждает в учениках любопытство.

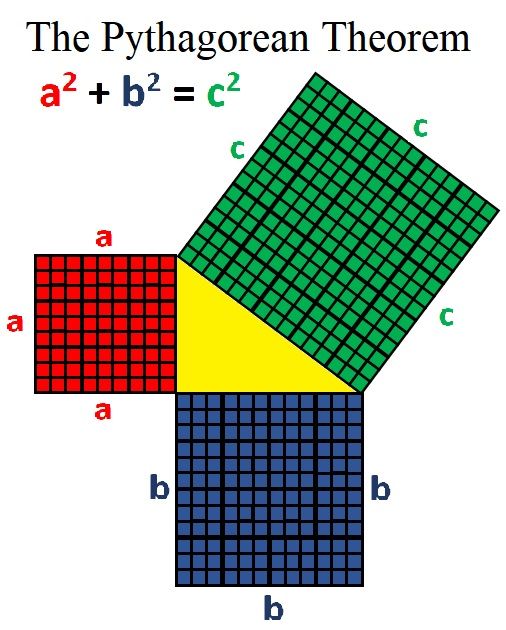
А если соединить вместе кубики разных размеров (грань на 9 квадратов, 16 и 25) может продемонстрировать теорему Пифагора, a2 + b2 = c2.